Density Based Clustering

Density-based clustering is a type of clustering algorithm that groups data points based on their density. Unlike other clustering algorithms, density-based clustering does not require a predefined number of clusters, and it can identify clusters of arbitrary shape and size. Here, we will explore density-based clustering in details.

The most well-known density-based clustering algorithm is called DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

DBSCAN works by defining two parameters:
epsilon (ε)
minimum points (minPts)
Epsilon is the radius around each data point within which other points are considered to be neighbors.
MinPts is the minimum number of points required to form a dense region, also known as a core point. The algorithm works by grouping together core points that are within epsilon distance of each other, and then expanding the cluster to include non-core points that are within the same epsilon radius.

---

Core Points

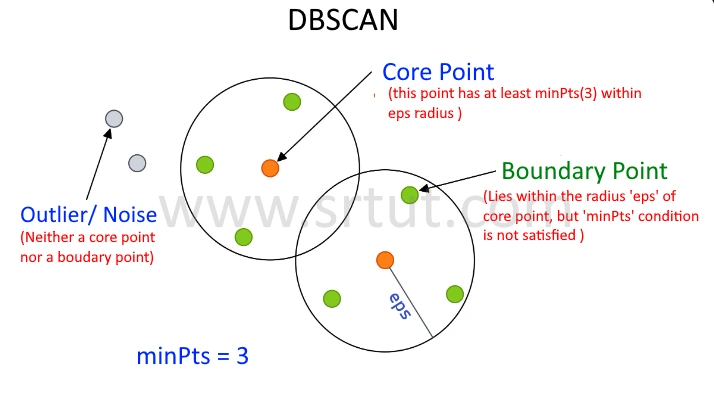
In clustering, the term "core point" typically refers to a data point that has a sufficient number of neighboring points within a certain distance, often referred to as the "radius" or "eps". The concept of core points is commonly used in density-based clustering algorithms, such as DBSCAN.

Core points are important because they help to identify dense regions of data points in a dataset, which are often interpreted as clusters. Points that are not core points but are still within the "eps" distance of a core point are referred to as "border points" and may be included in the same cluster as their corresponding core point. Points that are not core points and are not within the "eps" distance of any core point are considered "noise points" and are not included in any cluster.

---

---

Boundary Points

A boundary point is defined as a point that is within the "eps" distance of at least one core point, but does not have "minPts" other points within that same distance. Boundary points are not dense enough to be considered as core points, but they are still close enough to the cluster's core to be considered as part of the same cluster.

---

Noise Points

a noise point, also known as an outlier, is a data point that does not belong to any cluster in the result of a clustering algorithm. Noise points are typically located in sparse or low-density regions of the dataset and are not close enough to any other data points to be considered part of a cluster.

In many clustering algorithms, noise points are identified as data points that do not meet certain criteria for inclusion in a cluster. For example, in the DBSCAN clustering algorithm, noise points are defined as data points that are not within the "eps" distance of any core point and do not have "minPts" other points within that same distance.

Noise points can arise in clustering for a variety of reasons, such as measurement errors, data entry errors, or genuine anomalies in the data.

---

The DBSCAN algorithm proceeds as follows:

1. Select a random unvisited point from the data set.
2. Determine whether the point is a core point by counting the number of other points within epsilon distance of it.
3. If the point is a core point, create a new cluster and add all its neighbors (within epsilon distance) to the cluster.
4. Repeat the process for all the newly added points until no more points can be added to the cluster.
5. Mark all the points in the cluster as visited.
6. If the point is not a core point, mark it as noise.
7. Repeat the process for all unvisited points until all points have been visited.

---

One of the key advantages of density-based clustering is that it can identify clusters of arbitrary shape and size, unlike other clustering algorithms like k-means clustering, which assumes that clusters are spherical and have equal variance. Density-based clustering can identify clusters that are irregularly shaped, elongated, or have varying densities.

Advantages of density-based clustering

• Can identify clusters of arbitrary shape and size - Unlike other clustering algorithms like k-means, density-based clustering can identify clusters of arbitrary shape and size.
• Robust to noise and outliers - Density-based clustering can effectively handle noise and outliers by identifying them as individual data points that do not belong to any cluster.
• Does not require a predefined number of clusters - Density-based clustering does not require a predefined number of clusters, making it more flexible than other clustering algorithms.
• Can handle datasets with varying densities - Density-based clustering is effective at identifying clusters in datasets with varying densities.

Disadvantages of density-based clustering

1. Sensitivity to parameters - The performance of density-based clustering is highly dependent on the choice of the epsilon (ε) radius and the minimum number of neighbors required to define a core point. These parameters can be difficult to choose, and different choices can lead to different results.
2. Computationally expensive - Density-based clustering can be computationally expensive, especially for large datasets. The algorithm requires calculating distances between every pair of data points, which can be time-consuming for large datasets.
3. Can be sensitive to initialization - The performance of density-based clustering can be sensitive to the initial selection of core points. In some cases, the algorithm may converge to a suboptimal solution.

#density based clustering
import numpy as np
import pandas as pd
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
# load the dataset, load dataset as per yours
diabetes = pd.read_csv('diabetes.csv')
# select the features to be used for clustering
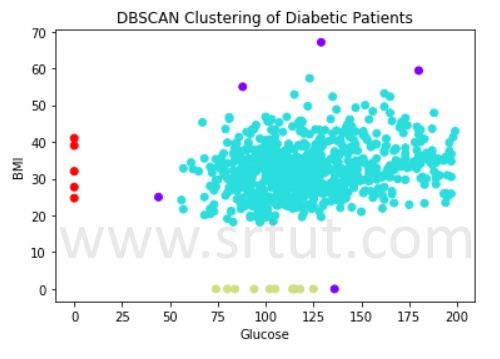
X = diabetes[['Glucose', 'BMI']]
# create a DBSCAN object and fit the data
dbscan = DBSCAN(eps=10, min_samples=3)
clusters = dbscan.fit_predict(X)
# create a scatter plot of the data points colored by their cluster assignments
plt.scatter(X['Glucose'], X['BMI'], c=clusters, cmap='rainbow')
plt.xlabel('Glucose')
plt.ylabel('BMI')
plt.title('DBSCAN Clustering of Diabetic Patients')
plt.show()

The output of the above code: