Naive Bayes Algorithm

Naive Bayes is a probabilistic algorithm used for classification tasks in machine learning. It is based on the Bayes theorem and assumes that the features used to classify instances are independent of each other. This assumption is known as the "naive" assumption and gives the algorithm its name.

The Naive Bayes algorithm works by calculating the probability of an instance belonging to a particular class based on the probability of each of its features given that class. The class with the highest probability is then chosen as the predicted class for the instance.

The algorithm can be divided into three main steps:

1. Training: In this step, the algorithm learns the probability of each feature given each class by analyzing a training dataset. The training dataset consists of labeled instances where each instance is associated with a class label.
2. Calculation of probabilities: After the training step, the algorithm uses the learned probabilities to calculate the probability of each feature given a new instance.
3. Classification: Finally, the algorithm combines the probabilities of each feature for each class to calculate the probability of the instance belonging to each class. The class with the highest probability is then chosen as the predicted class for the instance.

The Naive Bayes algorithm can be used for both binary and multi-class classification problems. There are three main types of Naive Bayes classifiers:

1. Gaussian Naive Bayes Classifier: This classifier is used for continuous data with a normal distribution. It assumes that the features follow a Gaussian or normal distribution. It calculates the mean and standard deviation for each feature in each class and uses them to predict the class probability of the new observation.
2. Multinomial Naive Bayes Classifier: This classifier is used for discrete data, such as text classification, where the feature vector represents the frequency of the occurrence of a word in the document. It assumes that the features are independent and follow a multinomial distribution. It calculates the probability of each feature in each class and uses them to predict the class probability of the new observation.
3. Bernoulli Naive Bayes Classifier: This classifier is also used for discrete data, but it assumes that the features are binary or Boolean variables, representing the presence or absence of a feature in the observation. It calculates the probability of each feature being present or absent in each class and uses them to predict the class probability of the new observation.

Example-1 of Naive Bayes algorithm

Suppose we have a dataset of emails, some of which are spam and others are not. Our goal is to classify new emails as either spam or not spam. We can use a Naive Bayes classifier to accomplish this task.

To apply the classifier, we first need to extract features from each email. These features can be anything from the words used in the email or the sender's email address. Let's say we choose the presence or absence of certain words as our features. We would create a feature vector for each email indicating which of our chosen words appear in that email.

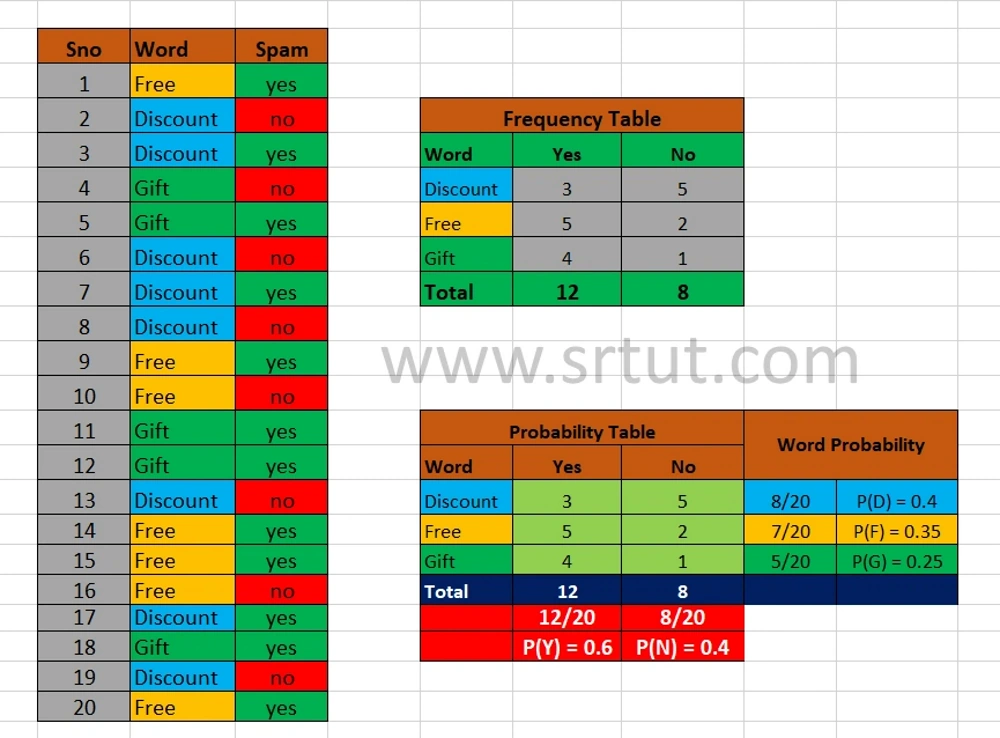
In the following image, Words like Discount, Free, Gift are taken from email dataset and their corresponding status is depicted. Then their frequency table is created. Frequency table contains count of occurence of each word with (Yes/No) Spam status. Now let us check whether a mail containing word Free is spam or not.
Let P(Y/Free) is the probability of the email being spam when it contains the word Free

Using Bayes theorem:
P(Y/Free) = [P(Y) * P(Free/Y)]/ [P(Free)]
P(Y/Free) = [(12/20)* (5/12)]/ [0.35]
P(Y/Free) = [(0.6)*(0.41)]/[0.35]
P(Y/Free) = [0.24]/[0.35]
P(Y/Free) = 0.68
Clearly, P(Y/Free) = 68%, So we can say that mail containing "Free" word has high probability of becoming spam. Hence Spam-class is allocated to this feature.

---

Example-2 of Naive Bayes algorithm

Suppose we have a dataset of customer reviews for a product, some of which are positive and others are negative. Our goal is to classify new customer reviews as either positive or negative based on the text content of the review.

To apply the classifier, we first need to preprocess the text data by converting the text into a feature vector. We can use techniques such as tokenization, stemming, and stop-word removal to extract meaningful features from the text. For example, we might extract individual words as features or groups of words that commonly occur together.

Next, we need to train our Naive Bayes classifier on a set of labeled data, i.e., customer reviews that we know are either positive or negative. The classifier will calculate the probability of each feature appearing in each class (positive or negative) based on the training data.

Finally, we can use the trained classifier to classify new customer reviews by calculating the probability of the review belonging to each class based on the features present in the review. The class with the higher probability is assigned to the review.

For example, if a new customer review contains the words "excellent," "great," and "awesome," the classifier is likely to assign a higher probability to the review being positive than negative. Conversely, if a new review contains the words "terrible," "poor," and "disappointing," the classifier is likely to assign a higher probability to the review being negative than positive.

Thus, the Naive Bayes algorithm can be used for text classification by converting text data into a feature vector and using probabilities to assign a class to each observation based on the probability of the features appearing in each class.

---

Advantages of Naive Bayes Algorithm:

There are several advantages to using the Naive Bayes algorithm:

1. Easy to implement: The algorithm is easy to understand and implement, making it a popular choice for many applications.
2. Fast and efficient: The algorithm is computationally efficient and can quickly classify new data points, even with large datasets.
3. Handles irrelevant features: The Naive Bayes algorithm assumes that the features are independent, which means that irrelevant features have no effect on the classification accuracy.
4. Handles missing values: The algorithm can handle missing data by ignoring the missing values during training.
5. Good performance: Despite its simplicity, the Naive Bayes algorithm often performs well compared to more complex algorithms, especially in text classification tasks.
6. No overfitting: The algorithm is less prone to overfitting compared to other more complex algorithms, as it has a high bias and low variance.

Overall, the Naive Bayes algorithm is a powerful and reliable classifier that is easy to implement, fast, and efficient. It is particularly useful for large datasets with a large number of features and is a popular choice for many applications, including email spam filtering, sentiment analysis, and document classification.

Limitations of Naive Bayes algorithm

Although the Naive Bayes algorithm has several advantages, it also has some limitations:

1. Independence assumption: The Naive Bayes algorithm assumes that the features are independent of each other, which is not always the case in real-world scenarios. This assumption can lead to incorrect classifications if the features are dependent on each other.
2. Zero-frequency problem: The algorithm cannot handle new features or feature values that were not seen during training. This problem is known as the zero-frequency problem and can be addressed by using smoothing techniques.
3. Limited expressive power: The Naive Bayes algorithm has limited expressive power compared to more complex algorithms, such as decision trees and neural networks. It may not be able to capture complex relationships between features and the target variable.
4. Imbalanced classes: The algorithm may not perform well when the classes are imbalanced, i.e., when one class has significantly more observations than the other.
5. Sensitivity to irrelevant features: Although the algorithm can handle irrelevant features, it may still be sensitive to them, which can affect its performance.
6. Gaussian assumption: In the case of the Gaussian Naive Bayes algorithm, it assumes that the features follow a Gaussian distribution, which may not be appropriate for all types of data.