Decision Tree

A decision tree is a supervised machine learning algorithm used for both classification and regression problems. It works by recursively partitioning the data into smaller subsets based on the features of the data, until a stopping criterion is met.

Algoritm

1. Start with the entire dataset D.
2. Choose a feature F from the dataset D based on some criterion, such as information gain , Gini impurity, or variance reduction.
3. Partition the dataset into subsets based on the values of the chosen feature F. Each subset becomes a node in the tree, and each node represents a split on a feature.
4. Recursively apply steps 2 and 3 to each subset until a stopping condition is met, such as a maximum depth or a minimum number of samples required to split a node.
5. Assign a label or a value to each leaf node based on the majority class or average value of the samples in that node.

Example Decision Tree Implementation

To understand the concept let's take an example. Suppose we have a dataset of 100 patients with the following features: age, gender, blood pressure, and cholesterol level, and we want to predict whether a patient has a heart disease or not. The target variable is binary: 0 indicates no heart disease, and 1 indicates heart disease.

We can build a decision tree as follows:

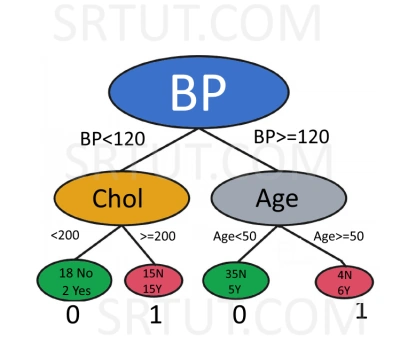
Start with the entire dataset D of 100 patients.

Choose a feature F based on some criterion, such as information gain , Gini impurity. Suppose we choose the blood pressure feature, which has the highest information gain.

Partition the dataset into two subsets based on the values of the blood pressure feature: BP < 120 and BP >= 120. We get two nodes: Node 1 (BP < 120) and Node 2 (BP >= 120).

For Node 1, choose another feature based on some criterion, such as information gain , Gini impurity. Suppose we choose the cholesterol level feature, which has the highest information gain. Partition Node 1 into two subsets based on the values of the cholesterol level feature: Chol < 200 and Chol >= 200. We get two leaf nodes: Leaf 1 (Chol < 200) and Leaf 2 (Chol >= 200). Assign a label to each leaf node based on the majority class in that node. Suppose Leaf 1 has 20 patients, out of which 18 have no heart disease and 2 have heart disease. Assign a label of 0 to Leaf 1. Suppose Leaf 2 has 30 patients, of which 15 have no heart disease and 15 have heart disease. Assign a label of 1 to Leaf 2.

For Node 2, choose another feature based on some criterion, such as information gain , Gini impurity. Now let us suppose, we choose the age feature, which has the highest information gain. Partition Node 2 into two subsets based on the values of the age feature: Age < 50 and Age >= 50. We get two leaf nodes: Leaf 3 (Age < 50) and Leaf 4 (Age >= 50). Assign a label to each leaf node based on the majority class in that node. Suppose Leaf 3 has 40 patients, of which 35 have no heart disease and 5 have heart disease. Assign a label of 0 to Leaf 3. Suppose Leaf 4 has 10 patients, of which 4 have no heart disease and 6 have heart disease. Assign a label of 1 to Leaf 4.

The decision tree is complete.

---

Decision trees can handle both categorical and numerical data, and can be used for both classification and regression tasks. They are easy to interpret and visualize, and can be used in ensembles such as random forests and gradient boosting.

---

---

Python implementation for Information Gain

import pandas as pd
from sklearn.datasets import load_iris
from sklearn.feature_selection import mutual_info_classif
# Load the Iris dataset
iris = load_iris()
# Create a Pandas DataFrame of the features
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)
# Calculate the information gain of each feature with respect to the target variable
ig_scores = mutual_info_classif(iris_df, iris.target)
# Print the information gain scores for each feature
for i in range(len(ig_scores)):
    print(f"Information gain of {iris.feature_names[i]}: {ig_scores[i]}")

Information gain of sepal length: 0.47563858603305653
Information gain of sepal width: 0.2913041668678975
Information gain of petal length: 0.9935512627152683
Information gain of petal width: 0.9874248909059007

This code calculates the information gain of each feature of the iris dataset: sepal length, sepal width, petal length, and petal width. The feature with the highest information gain is petal length.

---

Python implementation of Gini impurity

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
# Load the iris dataset
iris = load_iris()
X = iris.data
y = iris.target
# Initialize a decision tree classifier
clf = DecisionTreeClassifier()
# Train the classifier on the iris dataset
clf.fit(X, y)
# Calculate the Gini Impurity of all features
feature_importances = clf.feature_importances_
gini_impurities = [(1 - imp) for imp in feature_importances]
# Print the results
for i in range(len(iris.feature_names)):
    print(f"Gini Impurity of {iris.feature_names[i]}: {gini_impurities[i]}")

Gini Impurity of sepal length (cm): 1.0
Gini Impurity of sepal width (cm): 0.9866666666666667
Gini Impurity of petal length (cm): 0.4359440418679549
Gini Impurity of petal width (cm): 0.5773892914653784

This code provides, "gini_impurities" which is a list that calculates the Gini Impurity of each feature in the Iris dataset. The calculation is done by subtracting each feature importance value from 1.0. The feature with the lowest Gini impurity is petal length, which is the same feature with the highest information gain as calculated in the previous example.

To understand the concept, it is firstly necessary to understand what is "feature importance" in the context of a decision tree classifier. When a decision tree is trained on a dataset, the algorithm calculates the importance of each feature based on how much it contributes to the accuracy of the model. Features that split the data into subsets with high purity (i.e., all samples in a subset belong to the same class) are given higher importance.

The feature importance values returned by scikit-learn's "DecisionTreeClassifier" range from 0 to 1.0, where a value of 0 means that the feature was not used at all in the decision tree, and a value of 1.0 means that the feature perfectly splits the data into subsets with high purity.

In this code, "feature_importances" is a list containing the feature importance values for each feature in the Iris dataset. To calculate the Gini Impurity of each feature, we subtract the feature importance from 1.0. The reason for this is that the Gini Impurity is defined as a value between 0 and 1, where 0 represents perfect purity (i.e., all samples in a subset belong to the same class), and 1 represents maximum impurity (i.e., an equal number of samples from each class).

By subtracting the feature importance from 1.0, we effectively reverse the scale of the feature importance values so that higher importance values correspond to lower Gini Impurity values. This makes it easier to interpret the results, as it allows us to directly compare the Gini Impurity of each feature.