Shortcuts to Count Lines
Case-1
If there are n points on a circle (non-collinear), then total number of lines that can be drawn using all points, is given by:
Number of lines = [n X (n-1)] / 2
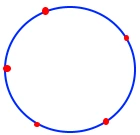
For example in the given diagram, total points = 5
So total lines = [5X(5-1)]/2 = [5X4]/2 = 20.
Note: If there are 'n' guests in a party, then same above technique can be used to find total number of handshakes = n X ( n-1 )/2
If there are 12 guests in a party then total handshakes
= (12 X 11)/2 = 66.
Case-2
If there are n points, out of which m are collinear (in same straight line), then total number of lines that can be drawn using all points, is given by:
Number of lines = [n X (n-1)] / 2 - [m X (m-1)] / 2 + 1
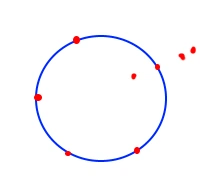
For example in the given diagram, total points = 8,
points in same straight line = 4.
So total lines = [8 X (8-1) ] / 2 - [ 4 X (4-1)] / 2 +1
= [8 X 7] / 2 - [4 X 3] / 2 +1 = 28 - 6 + 1
= 23
Case-3
If there are n points on a circle (non-collinear), then total number of triangles that can be drawn using all points, is given by:
Number of triangles = [n X (n-1) X (n-2)] / 6
For example in the given diagram, total points = 5
So total triangles = [5 X (5-1) X (5-2)] / 6 = [5 X 4 X 3]/6 = 10.

Case-4
If there are n points, out of which m are collinear (in same straight line), then total number of triangles that can be drawn using all points, is given by:
Number of triangles = [n X (n-1) X (n-2)] / 6 - [m X (m-1) X (m-2)] / 6
For example in the given diagram, total points = 8,
points in same straight line = 4.
So total triangles = [8 X (8-1) X (8-2) ] / 6 - [ 4 X (4-1) X (4-2)] / 6
= [8 X 7 X 6] / 6 - [4 X 3 X 2] / 6 = 56 - 4
= 52

Case-1
If there are n points on a circle (non-collinear), then total number of lines that can be drawn using all points, is given by:
Number of lines = [n X (n-1)] / 2
For example in the given diagram, total points = 5
So total lines = [5X(5-1)]/2 = [5X4]/2 = 20.
Note: If there are 'n' guests in a party, then same above technique can be used to find total number of handshakes = n X ( n-1 )/2
If there are 12 guests in a party then total handshakes
= (12 X 11)/2 = 66.

Case-2
If there are n points, out of which m are collinear (in same straight line), then total number of lines that can be drawn using all points, is given by:
Number of lines = [n X (n-1)] / 2 - [m X (m-1)] / 2 + 1
For example in the given diagram, total points = 8,
points in same straight line = 4.
So total lines = [8 X (8-1) ] / 2 - [ 4 X (4-1)] / 2 +1
= [8 X 7] / 2 - [4 X 3] / 2 +1 = 28 - 6 + 1
= 23

Case-3
If there are n points on a circle (non-collinear), then total number of triangles that can be drawn using all points, is given by:
Number of triangles = [n X (n-1) X (n-2)] / 6
For example in the given diagram, total points = 5
So total triangles = [5 X (5-1) X (5-2)] / 6 = [5 X 4 X 3]/6 = 10.

Case-4
If there are n points, out of which m are collinear (in same straight line), then total number of triangles that can be drawn using all points, is given by:
Number of triangles = [n X (n-1) X (n-2)] / 6 - [m X (m-1) X (m-2)] / 6
For example in the given diagram, total points = 8,
points in same straight line = 4.
So total triangles = [8 X (8-1) X (8-2) ] / 6 - [ 4 X (4-1) X (4-2)] / 6
= [8 X 7 X 6] / 6 - [4 X 3 X 2] / 6 = 56 - 4
= 52

Advertisement
Advertisement