Fast Shortcut Techniques to solve Aptitude Questions
Shortcuts for Train Aptitude Problems
To convert speed from Km per hour into metre per second
X (Km/hr) = X * (5/18) m/sec.
For example: 54 Km/hr = 54 X (5/18) = 15m/sec.
To convert speed from meter per second into Kilometer per hour
X (m/sec) = X * (18/5) km/ hour
For example: 20 m/sec. = 20 X (18/5) = 72 km/hour.
If a train is running at x km/hr, Convert it into meter/second. Let it be y m/sec. Then
Time take by it to cross a pole, tree or a man is, Time = 1/y second.
If x meters is the length of the train and s meter/sec is its speed, Then
Time taken by it to cross a platform or tunnel or bridge of length y meters is
time = (x+y)/s seconds.
If two trains A (length = x meters) and B (length = y meters) are running in opposite direction with speed s1 and s2 meters per second.Then time taken by them to cross each other is:
Time = (x+y)/(s1+s2) seconds
If same trains are moving in same direction, Then time taken to cross slow train by fast train is:
Time = (x+y)/(s1-s2), Here speed s1>speed s2
X (Km/hr) = X * (5/18) m/sec.
For example: 54 Km/hr = 54 X (5/18) = 15m/sec.
To convert speed from meter per second into Kilometer per hour
X (m/sec) = X * (18/5) km/ hour
For example: 20 m/sec. = 20 X (18/5) = 72 km/hour.
If a train is running at x km/hr, Convert it into meter/second. Let it be y m/sec. Then
Time take by it to cross a pole, tree or a man is, Time = 1/y second.
If x meters is the length of the train and s meter/sec is its speed, Then
Time taken by it to cross a platform or tunnel or bridge of length y meters is
time = (x+y)/s seconds.
If two trains A (length = x meters) and B (length = y meters) are running in opposite direction with speed s1 and s2 meters per second.Then time taken by them to cross each other is:
Time = (x+y)/(s1+s2) seconds
If same trains are moving in same direction, Then time taken to cross slow train by fast train is: Time = (x+y)/(s1-s2), Here speed s1>speed s2
Shortcuts for Clock Aptitude Problems
In these types of problems, Generally following sort of questions are asked.
- At a specific time, what is the angle between minute hand and hour hand?
- In some cases, angle is given and you have to find time at which that angle is formed.
- At what time the hour and and minute hands coincide that is come over each other?
- At what time the minute hand and hour hand will be at 90 degree angle?
- In a day how many times minute hand and hour hand coincide?
- In a day how many times minute hand and hour hand are at 90 degree?
Here are some shortcuts to answer these questions easily.
- In a day, hands of clock coincide(come over each other) = 44 times
- In a day, hands are in same straight line = 44 times.
- In a day, the hands are at right angle = 44 times
- 12/11 Rule :
This rule is used to solve questions like find the time when two hands of clock coincide or at right angle between two given times.
Note: To solve the questions first of all find the time gap between two hands
For example, At time 4 O'clock, time gap = 20 minutes (4 X 5 = 20). because hour hand is at 4 and minute hand at 12.
At time 3 O'clock, time gap = 15 minutes (3 X 5 =15). Because hour hand is at 3 and minute hand is at 12.
Now let us solve the question.
Ques 1) : At what time between 4 and 5 O'clock the hands will coincide?
Ans: Here time gap = 20 minutes.
Now time to overlap = (12/11) X 20 = 21.81 minutes.
So hands will coincide 21.18 minutes past 4.
Ques 2) : At what time between 2 and 3 O'lock, the hands of the clock are at right angle?
Ans : Here, It must be noticed that for 90 degree angle time gap = 15 minutes.
In the given question, time gap at 2:00 is 10 minutes.
So for right angle (90 degree) more time gap required = 5 minutes.
So required time = (12/11) X 5 = 10.90 past 2:00, the angle would be 90 degree.
- 30--6 Rule:
The angle between minute and hour hand = positive value of ( 30 X H - 6 X M)
Here H = number of hours and M = number of minutes in the time.
For example , Find the angle between two hands of clock at time 4:20.
First of all convert time 4:20 into hours.
So H = 4 + (20)/60 = (4+ 1/3) = 13/3 (here 20 is divided by 60 to convert 20 minutes into hours.)
Now angle = 30 X H - 6 X M
= 30 X (13/3) - 6 X 20 (here H = 13/3 and M = 20 minutes)
130 - 120 = 10 degree.
Note: If answer comes negative, ignore negative sign.
In these types of problems, Generally following sort of questions are asked.
- At a specific time, what is the angle between minute hand and hour hand?
- In some cases, angle is given and you have to find time at which that angle is formed.
- At what time the hour and and minute hands coincide that is come over each other?
- At what time the minute hand and hour hand will be at 90 degree angle?
- In a day how many times minute hand and hour hand coincide?
- In a day how many times minute hand and hour hand are at 90 degree?
- In a day, hands of clock coincide(come over each other) = 44 times
- In a day, hands are in same straight line = 44 times.
- In a day, the hands are at right angle = 44 times
- 12/11 Rule :
This rule is used to solve questions like find the time when two hands of clock coincide or at right angle between two given times.
Note: To solve the questions first of all find the time gap between two hands
For example, At time 4 O'clock, time gap = 20 minutes (4 X 5 = 20). because hour hand is at 4 and minute hand at 12.
At time 3 O'clock, time gap = 15 minutes (3 X 5 =15). Because hour hand is at 3 and minute hand is at 12.
Now let us solve the question.
Ques 1) : At what time between 4 and 5 O'clock the hands will coincide?
Ans: Here time gap = 20 minutes.
Now time to overlap = (12/11) X 20 = 21.81 minutes.
So hands will coincide 21.18 minutes past 4.
Ques 2) : At what time between 2 and 3 O'lock, the hands of the clock are at right angle?
Ans : Here, It must be noticed that for 90 degree angle time gap = 15 minutes.
In the given question, time gap at 2:00 is 10 minutes.
So for right angle (90 degree) more time gap required = 5 minutes.
So required time = (12/11) X 5 = 10.90 past 2:00, the angle would be 90 degree. - 30--6 Rule:
The angle between minute and hour hand = positive value of ( 30 X H - 6 X M)
Here H = number of hours and M = number of minutes in the time.
For example , Find the angle between two hands of clock at time 4:20.
First of all convert time 4:20 into hours.
So H = 4 + (20)/60 = (4+ 1/3) = 13/3 (here 20 is divided by 60 to convert 20 minutes into hours.)
Now angle = 30 X H - 6 X M
= 30 X (13/3) - 6 X 20 (here H = 13/3 and M = 20 minutes)
130 - 120 = 10 degree.
Note: If answer comes negative, ignore negative sign.
Shortcuts for Calendar Aptitude Problems
- A year having 365 days is called ordinary year.
- A year having 366 days is called leap year.
- The year divided by 4 is a leap year. For example 1984, 1996 etc.
- A century divisible by 400 is a leap year. For example 2000, 4000 etc.
- An ordinary year has 52 weeks and one extra day (also called one odd day).
- A leap year has 52 weeks and two extra days.
- In an ordinary year, Probability of 52 Sundays = 1/7 (May be any day)
- In a leap year, Probability of 52 Sundays = 2/7 (May be any day)
- If present year is not leap year, then next year, day will be incremented by 1. For Example if on 8th March 2022 is Tuesday, then 8th March 2023 will be Wednesday (2022 is not leap yr.)
If present year is leap year, day will be increamented by 2, if date falls till February month. Rest will be incremented by 1. For example: If on 12 February 2020 is Wednesday, then on 12 February 2021 is Friday (+2 increment Because date falls in the Feb. month). Where as if on 15 March 2020 is
Sunday, then on 15 march 2021 is Monday (+1 increament as date falls after Feb month).
- Last day of the century cannot be Tuesday, Thursday or Saturday.
- In a year, Calendar of March is repeated in November.
So, if on 12 March is Friday, then 12 November is also Friday.
- To solve the questions like: If today is Friday, what will be the day on 64th day?
Divide 64 by 7 and note the remainder. In this case, after dividing 64 by 7, remainder = 1
So if today is Friday, 64th day will be one more. that is Friday plus one = Saturday.
- Similarly, If today is Wednesday, what will be the day on 74th day?
Divide 74 by 7 and remainder = 4. So 74th day = Wednesday + 4 days = Sunday
Number Day
0 Sunday
1 Monday
2 Tuesday
3 Wednesday
4 Thursday
5 Friday
6 Saturday
- 100 years contain odd days = 5
- 200 years contain odd days = 5+5 = 10days = 1 week + 3odd days = 3 odd days
- 300 years contain odd days = 5+5+5 = 15days = 2 weeks + 1 odd days = 1 odd days
- 400 years contain odd days = 5+5+5+5 = 20days + 1(leap year day) = 3 weeks + 0 odd days
= 0 odd day
Ques : Find the day on 1st January 2001
Ans: Watch this video to know the method
- A year having 365 days is called ordinary year.
- A year having 366 days is called leap year.
- The year divided by 4 is a leap year. For example 1984, 1996 etc.
- A century divisible by 400 is a leap year. For example 2000, 4000 etc.
- An ordinary year has 52 weeks and one extra day (also called one odd day).
- A leap year has 52 weeks and two extra days.
- In an ordinary year, Probability of 52 Sundays = 1/7 (May be any day)
- In a leap year, Probability of 52 Sundays = 2/7 (May be any day)
- If present year is not leap year, then next year, day will be incremented by 1. For Example if on 8th March 2022 is Tuesday, then 8th March 2023 will be Wednesday (2022 is not leap yr.) If present year is leap year, day will be increamented by 2, if date falls till February month. Rest will be incremented by 1. For example: If on 12 February 2020 is Wednesday, then on 12 February 2021 is Friday (+2 increment Because date falls in the Feb. month). Where as if on 15 March 2020 is Sunday, then on 15 march 2021 is Monday (+1 increament as date falls after Feb month).
- Last day of the century cannot be Tuesday, Thursday or Saturday.
- In a year, Calendar of March is repeated in November.
So, if on 12 March is Friday, then 12 November is also Friday. - To solve the questions like: If today is Friday, what will be the day on 64th day?
Divide 64 by 7 and note the remainder. In this case, after dividing 64 by 7, remainder = 1
So if today is Friday, 64th day will be one more. that is Friday plus one = Saturday. - Similarly, If today is Wednesday, what will be the day on 74th day?
Divide 74 by 7 and remainder = 4. So 74th day = Wednesday + 4 days = Sunday
| Number | Day |
|---|---|
| 0 | Sunday |
| 1 | Monday |
| 2 | Tuesday |
| 3 | Wednesday |
| 4 | Thursday |
| 5 | Friday |
| 6 | Saturday |
- 100 years contain odd days = 5
- 200 years contain odd days = 5+5 = 10days = 1 week + 3odd days = 3 odd days
- 300 years contain odd days = 5+5+5 = 15days = 2 weeks + 1 odd days = 1 odd days
- 400 years contain odd days = 5+5+5+5 = 20days + 1(leap year day) = 3 weeks + 0 odd days
= 0 odd day
Ques : Find the day on 1st January 2001
Ans: Watch this video to know the method
Shortcuts for Percentage Aptitude Problems
To understand the tips of percentages consider the following cases:
- Ques: If price of a product is raised by R %, by how much percentage consumption should be reduced, so that expenditure remains same.
Tip: Consumption percentage reduction = (100 X R)/(100+R)
- Ques: If price of a product is reduced by R %, by how much percentage consumption should be increased, so that expenditure remains same.
Tip: Consumption percentage Increase = (100 X R)/(100-R)
- Ques: If A's salary is R % more than B's salary, by how much percentage B's salary is less than A's salary
Tip:Percentage of B's salary less than A's salary = (100 X R)/(100+R)
- Ques: If A's salary is R % less than B's salary, by how much percentage B's salary is more than A's salary
Tip:Percentage of B's salary more than A's salary = (100 X R)/(100-R)
- Ques: Let on an article, firstly D1% dicount is given, then D2 % discount is given then D3 % discount is given. Then the Equivalent discount of all these discounts is given by:
Tip: Equivalent Discount = 1 - [(100-D1%) X (100-D2%) X (100-D3%)]. Example
Tip: If on an article, firstly, A% discount is given then B % discount is given. Find equivalent discount.
Ans: Use the trick mentioned in the diagram.
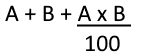
- Ques: Let P is the present population of a city and it increases at the rate of R% per annum
Tip: 1 Population after n years = P X (1+R/100) n
Tip: 2 Population n years ago = P / (1+R/100) n
- Ques: Let P is the present value of a product and it depreciates at the rate of R% per annum
Tip: 1 Cost of product after n years = P X (1-R/100) n
Tip: 2 Cost of product n years ago = P / (1-R/100) n
To understand the tips of percentages consider the following cases:
- Ques: If price of a product is raised by R %, by how much percentage consumption should be reduced, so that expenditure remains same.
Tip: Consumption percentage reduction = (100 X R)/(100+R) - Ques: If price of a product is reduced by R %, by how much percentage consumption should be increased, so that expenditure remains same.
Tip: Consumption percentage Increase = (100 X R)/(100-R) - Ques: If A's salary is R % more than B's salary, by how much percentage B's salary is less than A's salary
Tip:Percentage of B's salary less than A's salary = (100 X R)/(100+R) - Ques: If A's salary is R % less than B's salary, by how much percentage B's salary is more than A's salary
Tip:Percentage of B's salary more than A's salary = (100 X R)/(100-R) - Ques: Let on an article, firstly D1% dicount is given, then D2 % discount is given then D3 % discount is given. Then the Equivalent discount of all these discounts is given by:
Tip: Equivalent Discount = 1 - [(100-D1%) X (100-D2%) X (100-D3%)]. Example - Ques: Let P is the present population of a city and it increases at the rate of R% per annum
Tip: 1 Population after n years = P X (1+R/100) n
Tip: 2 Population n years ago = P / (1+R/100) n - Ques: Let P is the present value of a product and it depreciates at the rate of R% per annum
Tip: 1 Cost of product after n years = P X (1-R/100) n
Tip: 2 Cost of product n years ago = P / (1-R/100) n
Ans: Use the trick mentioned in the diagram.
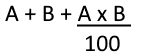
Shortcuts for Profit Loss Problems
To understand the tips of Profit loss consider the following terms
- S.P = Selling Price
- C.P = Cost Price
- Profit or Gain = S.P - C.P
- Loss = C.P - S.P
- Gain % = (Gain X 100) / C.P
- Loss % = (Loss X 100) / C.P
- S.P = [( 100+ Profit % ) X C.P] / 100
- S.P = [( 100- Profit % ) X C.P] / 100
- C.P = 100 X S.P / [ ( 100 + Profit % ) ]
- C.P = 100 X S.P / [ ( 100- Loss % ) ]
- If Profit percentage is give, Then S.P = ( 100 + Profit % ) X C.P
If an article is sold at 25% profit then S.P = 125 % of C.P
- If Loss percentage is give, Then S.P = ( 100 - Loss % ) X C.P
If an article is sold at 25% loss then S.P = 75 % of C.P
Formulas to find desired Profit or Loss
- If an article is sold for SP1 at profit P1 % then find the S.P to gain profit of P2 %
Here, substitute the values in the adjacent diagram and find the value of SP2.
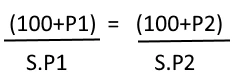
- If an article is sold for SP1 at Loss L1 % then find the S.P to gain profit of P1 %
Here, you should use the trick mention in the adjacent diagram.
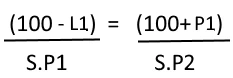
- If an article is sold at A % profit and then B % profit. What will be equivalent profit?
Here, you should use the trick mention in the adjacent diagram.
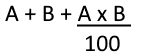
- If by selling two articles at same price, a person bears P% profit on one article and L% loss on other. Find overall profit or loss.
Use trick of adjacent diagram
Note: Positive answer means profit % and negative answer means Loss %.
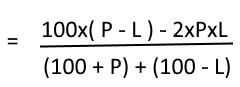
- If by selling two articles at same price, a person bears R% profit on one transaction and R% loss on other. Find overall profit or loss.
In this type of transaction there is always loss and loss percentage is given in adjacent diagram.
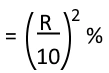
- If A sells an article to B at profit of X % and B sells it to C at profit of Y %. If C pays Rs. P then find cost price of A.
The cost price of A is given in adjacent diagram.
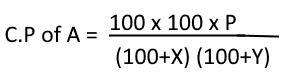
- If A sells an article to B at loss of X % and B sells it to C at loss of Y %. If C pays Rs. P then find cost price of A.
The cost price of A is given in adjacent diagram.
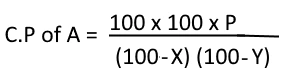
To understand the tips of Profit loss consider the following terms
- S.P = Selling Price
- C.P = Cost Price
- Profit or Gain = S.P - C.P
- Loss = C.P - S.P
- Gain % = (Gain X 100) / C.P
- Loss % = (Loss X 100) / C.P
- S.P = [( 100+ Profit % ) X C.P] / 100
- S.P = [( 100- Profit % ) X C.P] / 100
- C.P = 100 X S.P / [ ( 100 + Profit % ) ]
- C.P = 100 X S.P / [ ( 100- Loss % ) ]
- If Profit percentage is give, Then S.P = ( 100 + Profit % ) X C.P
If an article is sold at 25% profit then S.P = 125 % of C.P - If Loss percentage is give, Then S.P = ( 100 - Loss % ) X C.P
If an article is sold at 25% loss then S.P = 75 % of C.P
Formulas to find desired Profit or Loss
- If an article is sold for SP1 at profit P1 % then find the S.P to gain profit of P2 %
Here, substitute the values in the adjacent diagram and find the value of SP2.
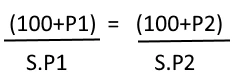
- If an article is sold for SP1 at Loss L1 % then find the S.P to gain profit of P1 %
Here, you should use the trick mention in the adjacent diagram.
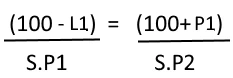
- If an article is sold at A % profit and then B % profit. What will be equivalent profit?
Here, you should use the trick mention in the adjacent diagram.
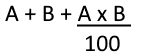
- If by selling two articles at same price, a person bears P% profit on one article and L% loss on other. Find overall profit or loss.
Use trick of adjacent diagram Note: Positive answer means profit % and negative answer means Loss %.
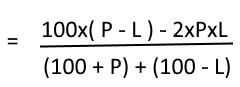
- If by selling two articles at same price, a person bears R% profit on one transaction and R% loss on other. Find overall profit or loss.
In this type of transaction there is always loss and loss percentage is given in adjacent diagram.
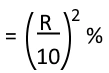
- If A sells an article to B at profit of X % and B sells it to C at profit of Y %. If C pays Rs. P then find cost price of A.
The cost price of A is given in adjacent diagram.
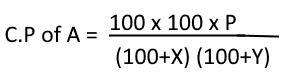
- If A sells an article to B at loss of X % and B sells it to C at loss of Y %. If C pays Rs. P then find cost price of A.
The cost price of A is given in adjacent diagram.
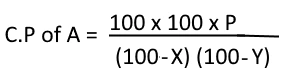
Shortcuts for Series Aptitude Problems
In these types of questions, some members of the series are given and you have to find the missing one.
For your reference some series are given and you have to keep these series in mind to solve these problems.
- Ques: Check for series of prime numbers.Prime numbers are those which are divisible by themselves or 1. For example: 2,3,4,5,7. 2 is the only even prime number.
Tip: Series: 2,3,5,7,11,13,17,19...
- Ques: Check for Fibonacci series. In this series, next number is obtained by adding previous two numbers.
Tip: Series: 0,1,1,2,3,5,8,13,21..., Clearly, next member is obtained by adding previous two members.
- Ques: Check for Powers of 2, 3, 5
Tip:Here you should check for 2n or 3n or 5n
For Example: 2,4,8,16,32....
3,9,27,81,243...
5,25,125,625,...
- Ques: Check for A.P(Arithmetic Progression). A.P means difference of any two numbers is same.
Tip: For Example: 3,8,13,18,23..., Clearly here common differnce is 5. So next element of series can be obtained by adding 5 to the previous number.
- Ques: Check for G.P (Geometric Progression) series. G.P means next number can be obtained by multiplying or dividing the previous member by a specific number.
Tip: For Example: 2,6,18,54,162..., Clearly here next member is obtained by multiplying the previous member by 3.
Similarly, in series, 81,27,9,3,1,1/3... next member can be obtained by dividing the previous member by 3.
- Ques: Check for Prime number minus one in the series.
For example: 1,2,4,6,10,12,16,18... Here the next member can be obtained by subtracting 1 from the next prime number.
Here the actual series was 2,3,5,7,11,13,17,19... (series of prime numbers.)
The given series is obtained by subtracting 1 from each member of prime number series.
- Ques: Check for Consecutive differences. These differences may be in AP, GP or Prime numbers as discussed above.
Tip: For example: 3,5,8,13,20,31,.., Here series obtained by finding consecutive difference is :
(5-3),(8-5),(13-8),(20-13),(31-20)
2, 3, 5, 7, 11. Which is a prime number series. So next number of the given series can be obtained by adding next prime number to the previous number.
Next prime number is 13, so the next number in the given series is = 13+31 = 44.
- Ques: Check for patterns changes.
Tip: For example: 12,21, 34,43, 89,98, 56,?
Here notice that next number can be obtained by reversing the digits of previous number. So here the next number is 65.
In these types of questions, some members of the series are given and you have to find the missing one.
For your reference some series are given and you have to keep these series in mind to solve these problems.
- Ques: Check for series of prime numbers.Prime numbers are those which are divisible by themselves or 1. For example: 2,3,4,5,7. 2 is the only even prime number.
Tip: Series: 2,3,5,7,11,13,17,19... - Ques: Check for Fibonacci series. In this series, next number is obtained by adding previous two numbers.
Tip: Series: 0,1,1,2,3,5,8,13,21..., Clearly, next member is obtained by adding previous two members. - Ques: Check for Powers of 2, 3, 5
Tip:Here you should check for 2n or 3n or 5n
For Example: 2,4,8,16,32....
3,9,27,81,243...
5,25,125,625,... - Ques: Check for A.P(Arithmetic Progression). A.P means difference of any two numbers is same.
Tip: For Example: 3,8,13,18,23..., Clearly here common differnce is 5. So next element of series can be obtained by adding 5 to the previous number. - Ques: Check for G.P (Geometric Progression) series. G.P means next number can be obtained by multiplying or dividing the previous member by a specific number.
Tip: For Example: 2,6,18,54,162..., Clearly here next member is obtained by multiplying the previous member by 3.
Similarly, in series, 81,27,9,3,1,1/3... next member can be obtained by dividing the previous member by 3. - Ques: Check for Prime number minus one in the series.
For example: 1,2,4,6,10,12,16,18... Here the next member can be obtained by subtracting 1 from the next prime number.
Here the actual series was 2,3,5,7,11,13,17,19... (series of prime numbers.)
The given series is obtained by subtracting 1 from each member of prime number series. - Ques: Check for Consecutive differences. These differences may be in AP, GP or Prime numbers as discussed above.
Tip: For example: 3,5,8,13,20,31,.., Here series obtained by finding consecutive difference is :
(5-3),(8-5),(13-8),(20-13),(31-20)
2, 3, 5, 7, 11. Which is a prime number series. So next number of the given series can be obtained by adding next prime number to the previous number. Next prime number is 13, so the next number in the given series is = 13+31 = 44. - Ques: Check for patterns changes.
Tip: For example: 12,21, 34,43, 89,98, 56,?
Here notice that next number can be obtained by reversing the digits of previous number. So here the next number is 65.
Shortcuts for Direction Aptitude Problems
Tip 1: While solving these problems, draw the diagram as shown in adjacent image.
Consider right hand side as East, Left Side West. Top North and bottom South.
Diagonal directions
(NE , SE, NW, SW) are also mentioned as shown.
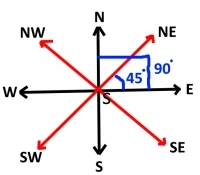
Tip 2:
You will always start your question with starting point origin that is S. Means consider yourself sitting at point S.
Tip 3:
Rotation of 180 degree in clockwise or anti-clockwise direction means you are pointing in opposite direction.
It means if your present face is towards east and now you rotate yourself through an angle of 180 degree, either clockwise or anti-clockwise. After Rotation
you will face towards West.
Tip 4:
Rotation of 45 degree in clockwise or anti-clockwise direction means you are facing in diagonal directions.
It means if your present face is towards east and now you rotate yourself through an angle of 45 degree clockwise. After Rotation
you will face towards South East (SE)
Tip 5:
Rotation of 90 degree in clockwise or anti-clockwise direction means you are turning towards right side or left side.
It means if your face is towards East and now you rotate left side, It means you rotate 90 degree towards anti-clockwise direction and now your face will be towards North.

Tip 6:
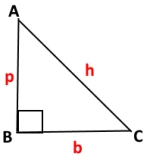
Using Pythagoras theorem
h2 = p2+ b2
Here p = perpendicular, b = base and h = hypotenuse.
Tip 1: While solving these problems, draw the diagram as shown in adjacent image.
Consider right hand side as East, Left Side West. Top North and bottom South.
Diagonal directions
(NE , SE, NW, SW) are also mentioned as shown.

Tip 2: You will always start your question with starting point origin that is S. Means consider yourself sitting at point S.
Tip 3: Rotation of 180 degree in clockwise or anti-clockwise direction means you are pointing in opposite direction. It means if your present face is towards east and now you rotate yourself through an angle of 180 degree, either clockwise or anti-clockwise. After Rotation you will face towards West.
Tip 4: Rotation of 45 degree in clockwise or anti-clockwise direction means you are facing in diagonal directions. It means if your present face is towards east and now you rotate yourself through an angle of 45 degree clockwise. After Rotation you will face towards South East (SE)
Tip 5: Rotation of 90 degree in clockwise or anti-clockwise direction means you are turning towards right side or left side. It means if your face is towards East and now you rotate left side, It means you rotate 90 degree towards anti-clockwise direction and now your face will be towards North.

Tip 6:
Using Pythagoras theorem
h2 = p2+ b2
Here p = perpendicular, b = base and h = hypotenuse.

Shortcuts for Simple Interest Aptitude Problems
If S.I= Simple Interest, R= Rate of interest
T = time, P = Principal,
Then formula of simple interest (S.I) and Amount (A) is given in adjacent image.
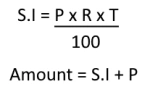
If certain sum of money becomes N times in T years, Then rate of interest is given by as shown.
For example, If certain sum of money becomes 4 times in 15 years at certain Simple rate of interest, then rate of interest is given by:
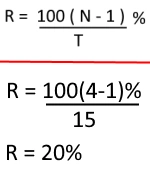
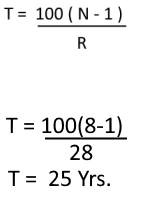
If certain sum of money becomes N times in T years at rate of interest R% , Then Time in years is given by as shown.
For example, If certain sum of money becomes 8 times at Simple rate of interest 28%, then Time is given by:
T = time, P = Principal,
Then formula of simple interest (S.I) and Amount (A) is given in adjacent image.
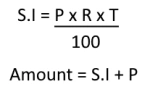
If certain sum of money becomes N times in T years, Then rate of interest is given by as shown.
For example, If certain sum of money becomes 4 times in 15 years at certain Simple rate of interest, then rate of interest is given by:
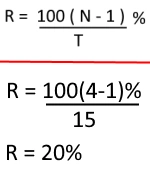
If certain sum of money becomes N times in T years at rate of interest R% , Then Time in years is given by as shown.
For example, If certain sum of money becomes 8 times at Simple rate of interest 28%, then Time is given by:

Shortcuts for LCM and HCF Aptitude Problems
-
HCF or GCD or GCM of two or more than two numbers is the greatest number that divides each one of them completely.
-
HCF calculation by Factorization: Each of the given number is expressed as the product of prime factors. Then the product of least powers of common prime factors is the HCF.
For example Find the HCF of 23X32X5X74, 22X35X52X73 and 23X53X72
Solution: The prime numbers common to the given numbers are 2, 5 and 7.
So HCF = 22X5X72 = 980.
- The H.C.F of two or more than two numbers is smaller than or equal to the smallest number of given numbers
- The LCM of two or more than two numbers is the least number which is exactly divisible by each one of the given numbers
- Product of two numbers = HCF of those two numbers X LCM of those two numbers.
-
The HCF of Fraction is given by:

-
The LCF of Fraction is given by:

Important Questions and Answers
-
Ques: Two numbers are in the ratio 17:11. If their HCF is 5. Find the numbers.
Ans: Let the numbers are 17x and 11x. Now their HCF = x.(Because x is common)
but the HCF = 5.
So the numbers are 17*5 = 85 and 11*5 = 55.
-
Ques: Find the largest four digits number exactly divisible by 12, 15, 18 and 27.
Ans: We know that largest four digits number is 9999. If it is divisible by all the given numbers, it means it should be divisble by LCM of given numbers.
LCM of given numbers = 540.
On dividing 9999 by 540, the remainder = 279.
So the smallest 4 digits number divisible by all the given numbers = 9999-279= 9720.
Ans: 9720.
- HCF or GCD or GCM of two or more than two numbers is the greatest number that divides each one of them completely.
-
HCF calculation by Factorization: Each of the given number is expressed as the product of prime factors. Then the product of least powers of common prime factors is the HCF.
For example Find the HCF of 23X32X5X74, 22X35X52X73 and 23X53X72
Solution: The prime numbers common to the given numbers are 2, 5 and 7.
So HCF = 22X5X72 = 980. - The H.C.F of two or more than two numbers is smaller than or equal to the smallest number of given numbers
- The LCM of two or more than two numbers is the least number which is exactly divisible by each one of the given numbers
- Product of two numbers = HCF of those two numbers X LCM of those two numbers.
-
The HCF of Fraction is given by:

-
The LCF of Fraction is given by:

Important Questions and Answers
-
Ques: Two numbers are in the ratio 17:11. If their HCF is 5. Find the numbers.
Ans: Let the numbers are 17x and 11x. Now their HCF = x.(Because x is common)
but the HCF = 5.
So the numbers are 17*5 = 85 and 11*5 = 55. -
Ques: Find the largest four digits number exactly divisible by 12, 15, 18 and 27.
Ans: We know that largest four digits number is 9999. If it is divisible by all the given numbers, it means it should be divisble by LCM of given numbers.
LCM of given numbers = 540.
On dividing 9999 by 540, the remainder = 279.
So the smallest 4 digits number divisible by all the given numbers = 9999-279= 9720.
Ans: 9720.
Shortcuts for Blood Relations Aptitude Problems
Sno. Symbol Relation
1 Brother--Brother
2 Sister--Sister
| Sno. | Symbol | Relation |
|---|---|---|
| 1 | Brother--Brother | |
| 2 | Sister--Sister |
Advertisement
Advertisement