Fast-maths-shortcuts-for rapid calculations-Srtut.com

Various Divisibility Tests

These technique are applicable for all integers

Divisibility Test 2: A number is divisible by 2, if right most digit present in the number is either zero or even digit
For Example: numbers 4343410 and 6834 are divisible by 2, because right most digits are 0 and 4(even digit).

Divisibility Tests 3 to 6

Divisibility Tests 6 to 15

Divisibility Test 3: A number is divisible by 3 if sum of the digits present in the number is divisible by 3.
For Example: 32451, here sum = 3+2+4+5+1 = 15, which is divisible by 3. So given number is divisible by 3.

Divisibility Test 4: A number is divisible by 4 if Right most two digit number of the given number is divisible by 4.
For Example: 8713636, Here right most two digit number is 36. Which is divisible by 4. So this complete number is divisible by 4.

Divisibility Test 5: A number is divisible by 5 if Right most digit is either zero or 5.
For Example: 548090 and 43785 ,Here right most digits are 0 and 5.So these numbers are divisible by 5.

Divisibility Test 6: A number is divisible by 6, if it satisfies the divisiblity test rules of 2 and 3.
that is right most digit is even or 0 and sum of digits should be divisible by 3.
For Example: 34152, Here right most digit is 2 which is even digit and sum of digits
3+4+1+5+2 = 15, which is divisible by 3. So Given number is divisible by 6.

Divisibility Test 8: A number is divisible by 8 if Right most three digits number of the given number is divisible by 8.
For Example: 87848848, Here right most three digits number is 848. Which is divisible by 8. So this complete number is divisible by 8.

Divisibility Test 9: A number is divisible by 9 if sum of the digits is divisible by 9.
For Example: 324513, here sum = 3+2+4+5+1+3 = 18, which is divisible by 9. So given number is divisible by 9.

Divisibility Test 10: A number is divisible by 10 if Right most digit is zero.
For Example: 548090 ,Here right most digits is 0 So this numbers is divisible by 10.

Divisibility Test 11: A number is divisible by 11 if sum of difference of even place digits and odd place digits is either 0 or multiple of 11
For Example: 942678, Here starting from left side,
odd place digits are: 9,2,7 and their sum = 9+2+7 = 18
Even place digits are: 4,6,8 and their sum = 4+6+8 = 18
Difference = 18-18 = 0. So the number 942678 is divisible by 11.

Divisibility Test 12: A number is divisible by 12, if it satisfies the divisiblity test rules of 3 and 4.
that is right most two digits number is divisible by 4 and sum of digits should be divisible by 3.
For Example: 31524, Here right most two digits number is 24 which is divisible by 4 and sum of digits, 3+4+1+5+2 = 15, which is divisible by 3. So Given number is divisible by 12.

Fast multiplication with 11

This technique is applicable for all integers

Consider following example

224321 X 11 Write first and last digit as it is in the answer
In the present case we will have 2_ _ _ _ _ _1
Now to fill in between blank spaces in the answer, starting from right hand side, find the sum of two digits and write in the answer
For Example 2+1= 3, So answer will take the shape 2_ _ _ _ _31
3+2= 5, So answer will become 2_ _ _ _ 531 like this.
So final answer is: 2467531

Fast Square Calculation

Square of two digits number with right most digit 5

This technique is used to find the square of two digit numbers with unit place digit 5

For example: to find 25² , 35² , 65²

For computing the square at fast speed, just write 25 on the the right hand side of the answer and product of left digit of the given number with its next digit and write the product on left side of the answer. Example: in case of 35, write __25 on the right hand side of the answer and next digit of left hand side digit(..ie 3) is 4, so we will write 3X4 on left hand side. So we will have 3X4 25 = 1225.

Similary for square of 65

6X7 = 42

and 25 on right hand side, we have 4225

Fast Percentage Calculation

Percentages

In order to compute percentages at fast speed consider following example

100 % of 36 is number itself ie.. 36
50 % of 36 is half of the number ie..18
25 % of 36 is one-fourth of the number ie..9
10 % of 36 is obtained by putting decimal point before right most digit of number ie..3.6
1 % of 36 is obtained by putting decimal point before two right most digits of number ie..0.36

Now let us compute some percentages

11% of 28 can be obtained like
10% of 28 + 1% of 28
2.8+0.28 = 3.08

51% of 42 can be obtained like
50% of 42 + 1% of 42
21+0.42 = 21.42

Fast Equivalent Discount Calculation

Equivalent Discount or Successive Discount

Note: Percentage means divide by 100. So 90% = 90/100 = 0.9

Let on an article, firstly D1% dicount is given, then D2 % discount is given then D3 % discount is given. Then the Equivalent discount of all these discounts is given by:

1 - [(100-D1%) X (100-D2%) X (100-D3%)].
Let successive discounts of 10%, 20% and 30% are given on an article whose price is 2000. Find Equivalent Discount and final price of article
Equivalent Discount = 1- [(100-10)% X (100-20)% X(100-30)%]
Equivalent Discount = 1 - [90% X 80% X 70%]
Equivalent Discount = 1-(0.90 X 0.80 X 0.70)
Equivalent Discount = 1-0.504 = 0.496 = 49.6%
Price = 0.496 X 2000 Rs.
Price = 992 Rs.

Fast Calculation Check Method

Fast Calculation Check

For this method consider 9 as zero in your mind.
and find the sum of digits of the given number in single digit format.
For example if we have a number 214,
In single digit format it is equivalent to 2+1+4 = 7
Similary, 548 = 5+4+8 = 17 = 1+7 = 8.Now I hope you understood the concept.
Now let us check the calculation of the diagram.

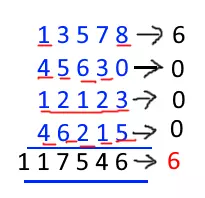
$fast-sum-calculation$

Here, four numbers and their sum is given. Now to check the calculation, write all the numbers in single in single digit format. Notice that first number in single digit format is 6 and rest of the
numbers each is equivalent to zero. Now compute the sum of all single digit numbers. Cleary, answer will be 6.
Now for correct calculation, the sum of all the digits in the actual answer should be 6 in single digit format. if it is, the calculation is correct.
here you will observe: 117546 = 1+1+7+5+4+6 = 6.
Hence the calculation is correct. Same method can be applied to multiplication, Subtraction also.

Fast Calculation square of 50 series

Square of 50 series

This method can be employed to find the square of 50 series. for example: 51², 52²
53² ... 59²
For example To find square of 53, write square of 3 in double digit format on right side of the answer it will be _ _09,
Now to fill left side of the answer, add 25 to 3 and write on the left side of the final answer.
25+3 = 28. So final answer is: 2809
Similary, we can find 58²
8² = 64, To be write on right hand side of answer
25+8 = 33
So, final answer is: 3364

Fast multiplication with 12

Multiplication with 12

This method is applicable to find the product of any number with 12.
For example we want to find the following product:
2341 X 12 = ?
Add a zero before the number.
we will have: 02341 X 12
Now starting from right hand side. double the digit and add to previous digit and write the answer.
Now here, right most digit is 1. Double this digit and write in the answer.
_ _ _ _ _ 2
now double the next digit and add it to previous digit. here next digit is 4
Now second digit is 4. Double it (become 8) and add it to previous digit that is 1, So it will become
8+1 = 9 write in the answer.
Now answere will be: _ _ _ _ 92. This process will continue and final answer will be : 28092

Fast Mathematical tips to speed up Calculations